2017年上半年教师资格证面试考试已经结束，考后真题及答案陆续发布中，请大家及时关注文都教师考试网，获取更新资讯。

　　高中数学《函数零点判定定理》

　　一、考题回顾

　　二、考题解析

　　高中数学《终边相同的角》主要教学过程及板书设计

　　教学过程

　　(一)创设情境、引入课题

　　下面有两组简笔画，哪一组说明人一定过河了?

　　第一组：

　　答辩题目解析

　　1.函数零点判定定理与二分法求零点之间有什么关系?【专业知识问题】

　　【参考答案】

　　通过不断地把连续函数f(x)的零点所在的区间一分为二，使区间的端点逐步逼近零点，进而得到零点近似值的方法叫做二分法。由此可见，函数零点判定定理是二分法求零点的理论依据和前提。

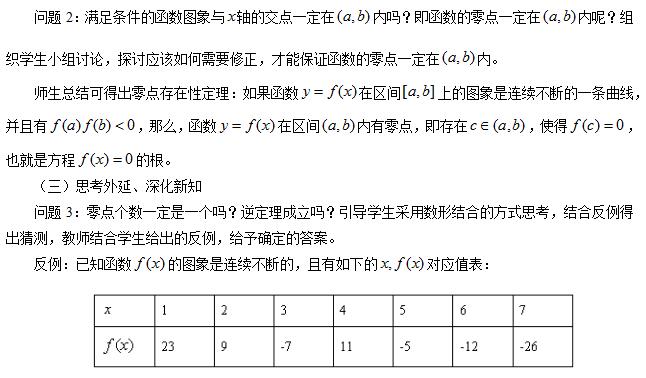
　　2.如果一个连续函数在定义域内是单调函数，那么函数的零点的个数可以确定吗?【专业知识问题】

　　【参考答案】