二、简答题(满分12分)

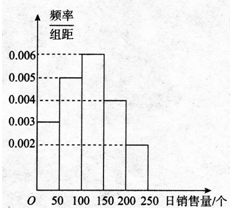
　　把某公司一种产品的销售记录绘制出日销售量的频率分布直方图，如图所示，将日销售量

　　落入各组的频率视为概率，并假设每天的销售量相互独立.

　　(1)求在未来连续3天里，有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率;

　　(2)用X表示在未来3天里日销售量不低于100个的天数，求随机变量X的分布列、数学期望E(X)及方差D(X).

　　三、案例分析题(满分14分)

　　下面是《勾股定理》一课的教学片断.

　　【新课导入】听故事，想问题.相传2500多年前，古希腊数学家毕达哥拉斯去朋友家做客.宴席上，其他宾客在尽情欢乐，毕达哥拉斯却盯着朋友家的地面方砖发呆.原来，地砖铺成了由许多个直角三角形组成的图案，黑白相间，非常美观.主人在纳闷时，毕达哥拉斯突然恍然大悟，原来，他发现了图案中三个正方形的面积存在某种数学关系.图中三个正方形的面积之间含着怎样的数量关系呢?让我们一起探索吧!

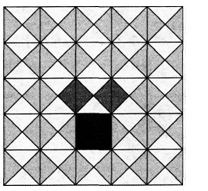
　　【后续教学环节】接下来，在老师的引导下，进行小组合作学习.同学们发现了以等腰直角三角形两直角边为边长的小正方形的面积和等于以斜边为边长的大正方形的面积，即等腰三角形三边之间有特殊的关系.斜边的平方和等于两直角边的平方和.接下来，在网格中探究得到其他的直角三角形也有上述性质，由此猜想出勾股定理.

　　根据以上材料，请回答下列问题：

　　1.从教学方法角度分析该课的新课引入的教学方法及其合理性;

　　2.从教材把握的角度分析《勾股定理》一课在初中数学教学的地位与作用;

　　3.从三维课程目标的角度分析上述教学设计落实了哪些教学目标.

　　四、教学设计题(满分14分)

　　教学内容：探索并证明“三角形内角和定理”

　　(学习基础：已经学习了相交线、平行线性质及其判定).

　　撰写要求：

　　1.只写出探索和证明两个环节的教学设计片段;

　　2.说明每个教学环节的设计意图.